Ao ensinar teoria dos jogos aos seus noviços, os professores de microeconomia tendem geralmente a ensinar jogos simples. É comum que o aluno termine sua cadeira aprendendo (ou pelo menos supostamente) a lidar com matrizes de jogos do seguinte tipo:
É esperado que todo aluno tenha capacidade de resolver esse tipo de jogo ao completar seu curso. O que deve ser notado sobre essa matriz é que ela é relativamente simples. Sim, caro aluno, essa coisa que você sofreu tanto para resolver em suas provas é algo relativamente fácil de resolver…
O jogo acima é um clássico jogo de dois jogadores com duas estratégias ou, como os teóricos dos jogos chamam em sua incrível criatividade, um jogo 2 x 2. A incrível facilidade e irrealidade de um jogo assim é que dificilmente uma pessoa tem que lidar apenas com duas estratégias. Na maioria do tempo as pessoas tem que lidar com mais de um par de escolhas contra um possível oponente. É ai que as coisas começam a ficar divertidas!
Quando computamos jogos com mais de duas estratégias as complexidades começam a aparecer e as soluções ficam mais complicadas. Para exemplificar o meu ponto irei ilustrar o caso com jogo mais simples criado pela humanidade: Pedra, Papel e Tesoura. Todos já jogaram esse jogo pelo menos uma vez na vida e não se preocupe, não irei fazer aqui uma disputa de vida e morte como em Hunter vs Hunter.
O que deve ser notado em jogos como Pedra, Papel e Tesoura é que, primeiramente, ele é um jogo de soma-zero. Ou você vence ou você perde, não existe payoff intermediário positivo para o jogador perdedor. Essa característica do jogo é bastante útil para nosso propósito didático, pois simplifica mais nossa análise. A segunda coisa a ser notada é que esse é, obviamente, um jogo de três estratégias.
Jogos do tipo 3 x 3 são mais complicados de se resolver do que jogos do tipo 2 x 2. Para não lhe traumatizar, vamos começar por um exemplo extremamente fácil de se resolver. Na matriz abaixo temos um jogo de soma-zero de três estratégias:
Como se trata de um jogo de soma-zero e por uma questão de simplificação, apenas os payoffs do jogador principal são computados. Naturalmente iremos começar nossa análise observando se o jogo possui um saddle-point por meio de uma solução minmax. Utilizando esse método de resolução encontramos que:
Encontramos um saddle-point! A estratégia ótima dos jogadores nesse jogo hipotético será escolher suas estratégias de forma que ambos terminarão com o payoff de 0 (um jogo justo). O valor do jogo para ambos os jogadores também será de 0, o que mostra que ambos serão indiferentes a jogar ou não o jogo por uma mera questão de ganho.
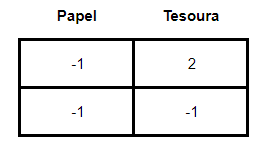
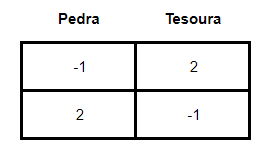
Todavia, as coisas ficam mais complicadas quando analisamos o “simples” jogo de Pedra, Papel e Tesoura. A matriz desse jogo é dada da seguinte forma:
Onde os payoff são dados como:
◉ 1 = vitória
◉ 0 = empate
◉ - 1 = derrota
Até ai um jogo aparentemente simples. Como se trata de um jogo de soma-zero, vamos tentar primeiramente resolvê-lo por meio de um minmax. O que encontramos ao tentar realizar essa solução é:
Note que não existe um saddle-point para os jogadores, de forma que a solução via minmax não serviu para o jogo. Quando isso ocorre em jogos de soma-zero é necessário tentar uma solução de estratégias mistas por meio de dominância. O método de dominância consiste em comparar, célula por célula, os payoffs dos jogadores e encontrar aquela estratégia que apresenta um resultado melhor do que as outras. Quando essa estratégia é encontrada, para o caso do jogador principal, as estratégias dominadas são excluídas da matriz ou, para o caso do jogador rival, as estratégias dominantes são excluídas. Como resultado, temos uma simplificação da matriz de jogo de uma 3 x 3 para uma 2 x 2 ou uma 2 x n. Ai fica mais fácil do aluno responder.
Contudo, no caso do jogo de Pedra, Papel e Tesoura isso não é uma possibilidade de solução. Note, caro leitor, que não existe dominância na matriz acima, pois a comparação célula por célula não revela nenhuma estratégia superior às outras (em verdade, as estratégias são simétricas!). Bem, nesse caso teremos que recorrer a um método bem mais exótico de resolução de jogos que irei ensinar abaixo…
Para solucionar o jogo abaixo primeiramente temos que subtrair a primeira linha ou a primeira coluna das linhas e colunas seguintes, a depender se estamos analisando o jogo a partir do ponto de vista do jogador principal (colunas) ou do jogador rival (linhas). Vamos imaginar que somos o jogador principal e estamos tentando analisar as possíveis estratégias do jogador rival. Nesse caso, o primeiro passo da solução do jogo passa pela subtração das linhas pelas linhas imediatamente posteriores, obtendo a matriz abaixo:
O que fazemos em seguida é calcular as chances de cada estratégia. Para realizar isso escolhemos entre as três estratégias (Pedra, Papel ou Tesoura) e isolamos a que estamos analisando. Se estivermos analisando as chances da estratégia “Pedra”, então teríamos a seguinte simplificação da matriz acima:
Em seguida realizamos uma multiplicação dos payoffs em diagonal e os subtraíamos. Fazendo isso para o exemplo acima da estratégia “Pedra” teríamos que:
(-1) x (-1) - ((-1) x 2) = 3
Assim, as chances da estratégia “Pedra” seriam iguais a 3. Fazendo o mesmo para “Tesoura” temos que:
(-1) x (-1) - ((-1) x 2) = 3
E para “Papel”:
(-1) x (-1) - 2 x 2 = -3
Uma vez que as chances não podem ser negativas, podemos desconsiderar o sinal do - 3 e computá-lo como 3. Dessa forma as chances das estratégias do jogador rival são 3:3:3. Entretanto, caro leitor, lembre que as estratégias dos jogadores de Pedra, Papel e Tesoura são simétricas. Assim, as chances para as estratégias do jogador principal também são 3:3:3. Dessa forma podemos computar as chances na nossa matriz de jogo como:
Note, caro leitor, que podemos simplificar ainda mais essa matriz. As chances podem ser simplificadas dado que possuem um multiplicador comum (3). Realizando a divisão temos que as chances de cada jogador serão 1:1:1.
Assim, cada jogador terá que combinar suas estratégias segundo as chances de 1:1:1. Ou seja, a escolha racional deles será utilizar….qualquer uma das estratégias! Não existe uma resposta clara para qual deve ser para qual deve ser a estratégia adotada pelo jogador. Não estranhamente se calcularmos o valor desse jogo para qualquer um dos jogadores teremos que:
(1 x 0) + (1 x -1) + (1) / 3 = 0
Um jogo de payoff igual a 0 e, portanto, um jogo justo para ambos os jogadores (ninguém perde e ninguém ganha na média).
A grande questão do jogo de Pedra, Papel e Tesoura (além do método de solução) é que qualquer modificação das chances de um dos jogadores pode afetar o valor do jogo. Como observou um post recente no Less Wrong, caso um dos jogadores tenha uma chance maior do que o outro em uma das estratégias (se ele fizer uma poker face ou dissuadir seu oponente) então o jogo fica desequilibrado; com o jogador melhorando seu payoff mas tornando o jogo menos interessante de ser jogado ao mesmo tempo!
Complicado, não?
BÔNUS: PRÁTICA COM PYTHON
Como vimos, um jogo de Pedra, Papel e Tesoura sempre tende a atingir uma forma de equilíbrio justo quando o jogador não possui formas de dissuadir o outro jogador; com técnicas como poker face ou conversação. Todavia, isso é claramente um jogador não-humanos. Humanos sempre terão a possibilidade de usar de assimetria de informação e blefe para mudar o equilíbrio do jogo.
Por essa razão, que tal testar nossa hipótese do equilíbrio justo dado a aleatoriedade e imprevisibilidade dos resultados do Pedra, Papel e Tesoura com um computador? Para isso vamos utilizar de um programa em linguagem Python que cria uma simulação de computador do jogo de Pedra, Papel e Tesoura.
Segue o código para quem quiser jogar com o computador:
# Aqui temos um código de um jogo simples de Pedra, Papel e Tesoura em Python
import random
def ppp():
jogador = input("Escolha uma opção: 'pedra', 'papel' ou 'tesoura'\n")
computador = random.choice(['pedra', 'papel', 'tesoura'])
if jogador == computador:
return 'Empate!!! 🤝'
if vitoria_ppp(jogador, computador):
return "Você ganhou!!! ♛"
return 'Você perdeu!'
def vitoria_ppp(voce, oponente):
if (voce == 'papel' and oponente == 'pedra') or (voce == 'tesoura' and oponente == 'papel') or \
(voce == 'pedra' and oponente == 'tesoura'):
return True
print(ppp())
BIBLIOGRAFIA:
— MORGENSTEN, Oskar; VON NEUMANN, John. Theory of Games and Economic Behavior. Princenton Univeristy Press, 2007;
— DRESCHER, Melvin. The Mathematics of Games of Strategy. Dover Publication, 1981.